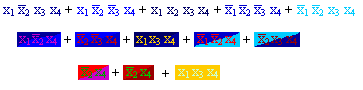http://www.oelinger.de     Home Maria Oelinger       zurück zur Übersicht     Teil I   Teil II 2.2 Vereinfachung von Schaltnetzen   Resolutionsregel Kommen in der DNF 2 Summanden vor, die sich in genau 1 Variablen unterscheiden (also x i, ¬x i), so können sie ersetzt werden durch ihren gemeinsamen Teil.   Beispiel a)  x1 x2 x3 + x1 ¬x2 x3 = x1 x3 (x2 + ¬x2) = x1 x3 • 1 = x1 x3 b)  Es folgt: f = ¬x2 x4 + x1 x3 x4 Wichtig Die Resolutionsregel darf mehrfach auf einen Summanden angewendet und auch iteriert werden! Wegen x = x + x   Karnaugh-Diagramm K-Diagramm zu f: BnB mit n  {3, 4} ist die graphische Darstellung der Funktionstabelle von f wie folgt: 0-1-Matrix der Größe bzw. 2 × 4 4 × 4 (n = 3) (n = 4) mit Spalten, die die möglichen Belegungen von x1 und x2 enthalten und Zeilen, die die möglichen Belegungen von x3 bzw. x3 und x4 enthalten. Die Reihenfolge der Beschriftung ist die, dass sich zwei zyklisch benachbarte Spalten oder Zeilen in genau 1 Komponente unterscheiden, also: n = 4   n = 3     x1 x2   x1 x2 x3 x4   0 0 0 1 1 1 1 0 0 0         0 1         1 1         1 0         x3   0 0 0 1 1 1 1 0 0         1         Ist f für eine Belegung von     x1, …, x3     bzw. x1, …, x4     gleich 1, so wird diese 1 in das Diagramm an entsprechender Stelle eingetragen.   Regel Jede 1 muß von mindestens einem Block überdeckt werden. Ziel: Möglichst große Blöcke. Dann folgt: Ein Block mit 2k Einsen liefert einen Term mit (n – k) Variablen. (s. Beispiel)   weiter...   zurück zur Übersicht Feel free to send me email: maria@oelinger.de
	© 2000 Maria Oelinger cand. math. Schaltungen und Boolesche Algebra (15) Letzte Änderung: 19.11.2000 address: http://www.oelinger.de/maria/schalt/schalt15.htm