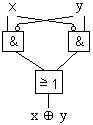
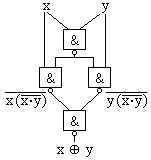
http://www.oelinger.de     Home Maria Oelinger       zurück zur Übersicht     Teil I   Teil II   Teil III 2. Spezielle Schaltnetze 2.1 Beispiele von Schaltnetzen   NAND-Gatter NAND- bzw. NOR-Gatter reichen aus, um Boolesche Funktionen aufzubauen, d.h. sie sind vollständig. Beispiel Dasselbe mit NANDs: Beweis NAND bedeutet:   ¬x • y XOR   x  y = x•¬y + ¬x•y = x•(¬x + ¬y) + y•(¬x + ¬y) = x•¬(x•y) + y•¬(x•y) = ¬[¬(x•¬(x•y))] + ¬[¬(y•¬(x•y))] = ¬[¬(x•¬(x•y))•¬(y•¬(x•y)]   de Morgan    NAND   Ziel Schaltung für die Addition von 16-Bit-Zahlen x = x15 … x0 und y = y15 … y0. Die Summe ist     x + y = z16 … z0.        z16 für potentiellen Überlauf   Aufwand Es gibt 2 32 > 10 9   Werte im Definitionsbereich, etwa die Hälfte mit dem Wert 1: 17•2 31   Terme in der DNF. 3.4•10 10   Minterme.   Majoritätsfunktion maj (x1, y1, r0) := x1y1 + r0 (x1  y1)   praktischer Ansatz Rekursive Addition mit XOR. Binärsystem: x = xn-1 … x0 und y = yn-1 … y0   mit xi, yi  B. a) Berechne x0  y0 = z0 x0 • y0 = r0 Übertrag b) Berechne x1  y1  r0 = z1 r1 = maj (x1, y1, r0) x y r z r = maj (x, y, r) 0 0 0 0 1 1 1 1 0 0 1 1 0 0 1 1 0 1 0 1 0 1 0 1 0 1 1 0 1 0 0 1 0 0 0 1 0 1 1 1 weiter...   zurück zur Übersicht Feel free to send me email: maria@oelinger.de
	© 2000 Maria Oelinger cand. math. Schaltungen und Boolesche Algebra (12) Letzte Änderung: 19.11.2000 address: http://www.oelinger.de/maria/schalt/schalt12.htm