zurück zum Überblick

http://www.oelinger.de Home Maria Oelinger   sitemap

Entropie und Wahrscheinlichkeit

Entropiefunktion

H: _n – 1R⁺

mit _n – 1 = { {p₁, …, p_n} | 1  p_i  1   und   _i=1,…,n p_i = 1 }

Axiome

1. H ist stetig

2. H (1/n, …, 1/n)  H (1/n+1, …, 1/n+1)   (je n- bzw. (n+1)-mal)

3. H (1/n, …, 1/n) = H (b₁/n, …, b_k/n) + _i=1,…,k b_i/n • H (1/b_i, …, 1/b_i)   (b_i-mal)

   für b_i  N,     _i=1,…,k b_i = n     und für     S = _i=1,…k B_i     mit     |B_i| = b_i

Eigenschaften

1. System von Funktionen auf _n – 1  R⁺, also H: _n – 1  R⁺

2. 0  H (p₁, …, p_n)  log n

3. P = {p₁, …, p_n }, Q = {q₁, …, q_n } mit  p_i = 1 und  q_i  1. Dann gilt:
   H (p₁, …, p_n)  H (q₁, …, q_n)

4. P = {p₁, …, p_n, q₁, …, q_m } mit  p_i = a und  q_i = 1 – a. Dann gilt:
   H (P) = H (a, 1 – a) + a • H (p₁/a, …, p_n/a) + (1 – a) • H (q₁/1-a, …, q_m/1-a)

5. H ist konkav: Für P = {p₁, …, p_n}, Q = {q₁, …, q_m } mit      p_i = 1 =  q_j     ist

   H ( • (p₁, …, p_n) + (1 – ) • (q₁, …, q_m))   • H (p₁, …, p_n) + (1 – ) • H (q₁, …, q_m)

   

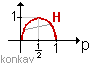
r-näre Entropie
H_r (p₁, …, p_n) = – _i=1,…,n p_i • log _r p_i = + _i=1,…,n p_i • log _r 1/p_i     mit Basis r > 1 und p  log p = 0 für p = 0.

ideale Entropie
Falls eine Quelle (S, P) zu einer r-nären Entropie existiert.

Feel free to send me email: maria@oelinger.de