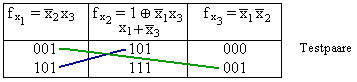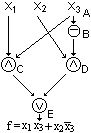
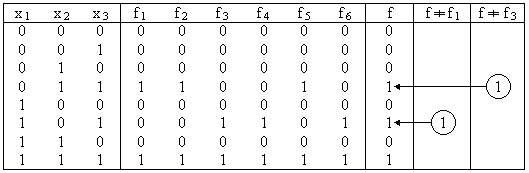
http://www.oelinger.de     Home Maria Oelinger       zurück zur Übersicht     Teil I   Teil II 2.4 Fehlerdiagnose   Beispiel f (x) = x1 x3 + x2 x3 mit zugehörigem 2-stufigen Netz: 6 Drähte. Fehlerannahme Ein Draht ist gerissen. fi sei die Funktion, in der der Draht i defekt ist: f1 = 0 • x3 + x2 x3     = x2 x3   = f2 = f5   f3 = x1 x3 = f4 = f6 Damit läßt sich die Wahrheitstafel aufstellen: Zur Erkennung des Eintragfehlers reichen die Tests mit den Belegungen 011 und 101, d.h. zwei Kombinationen statt acht. FAZIT Diese Methode ist inpraktikabel.   Testpaar Testpaar für Variable xi ist a, b  Bn, wenn sich a und b nur an der i-ten Stelle unterscheiden und f (a)  f (b). Test n-Tupel a  Bn.   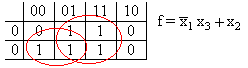minimale Testmenge Minimale Testpaarmenge ist die Menge T mit der geringsten Anzahl von Testpaaren für jedes xi, von dem f abhängt: f abhängig von xi   <=>   fxi = 1 Beispiel f: B3B mit f (x) = ¬x1 x3 + x2 f ist abhängig von x1, denn der Wert ändert sich beim Wechsel von x1: f (0, 0, 1) = 1 und f (1, 0, 1) = 0 Das Testpaar {(0, 0, 1), (1, 0, 1)} erkennt den Defekt, der die Abhängigkeit von x1 zerstört. Karnaugh: Ringsummenform f  = x2  ¬x1 x3  ¬x1 x2 x3 = x2  ¬x1 ¬x2 x3 Minimale Testmenge ist hier {(0, 0, 0), (0, 0, 1), (1, 0, 1), (1, 1, 1)} oder {(0, 0, 0), (0, 1, 0), (1, 0, 1), (0, 0, 1)}.   weiter...   zurück zur Übersicht Feel free to send me email: maria@oelinger.de
	© 2000 Maria Oelinger cand. math. Schaltungen und Boolesche Algebra (19) Letzte Änderung: 19.11.2000 address: http://www.oelinger.de/maria/schalt/schalt19.htm