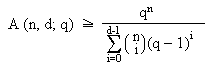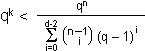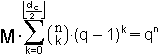http://www.oelinger.de Home Maria Oelinger   sitemap
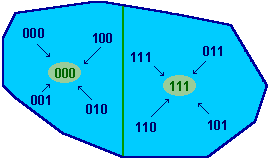
	zurück zum Überblick Schranken für die Mächtigkeit von Codes Codeteich d = 1 ermöglicht Schranke für Entscheidung   Rate R =     Aq (n, d) Aq (n, d) = A (n, d; q) = Max {M | ein q-närer (n, M; dC)-Code existiert} Also ist eine möglichst große Rate gesucht, d.h. mächtige Codes, die viel Information enthalten. für alle n  1: Aq (n, 1) = qn d.h. der gesamte Codeteich (= Wortmenge) ist Codewortmenge Aq (n, n) = q      Wiederholungscode für alle n  2: Aq (n, d)  q • Aq (n – 1, d) für binäre Codes: A2 (n, 2t + 1) = A2 (n + 1, 2t + 2)   Singleton-Schranke Aq (n, d)  qn–d+1   Gilbert-Varshamov-Schranke Diese Schranke ist nicht scharf.   Satz von Gilbert-Varshamov Ein [n, k, d, q]-Code existiert, wenn gilt: Diese Schranke ist scharf.   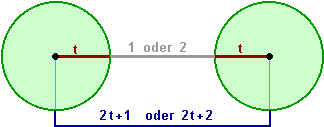Satz von Plotkin Gilt     und     d >  • n,     so folgt:   Kugelpackungssatz Mit d = 2t + 1 gilt:   Codewortumgebungskugeln Codewörter mit Umgebung S (x, t) := { y  An | d (x, y)  t }    für x  C.       C ist Code.   packing radius pr (C) ist der größte Radius, für den alle Codewort-Umgebungskugeln disjunkt sind.   covering radius cr (C) ist der kleinste Radius, für den alle Codewort-Umgebungskugeln ganz An überdecken. Klar: pr (C)  cr (C)   perfekt heißt ein Blockcode C  An, wenn     pr (C) = cr (C) quasi-perfekt heißt ein Code, wenn     pr (C) = cr (C) – 1, d.h. die Kugeln überlappen sich nur um 1 Element.   Kugelpackungsbedingung C sei q-närer (n, M, dC)-Code. Dann gilt: C ist perfekt genau dann, wenn gilt: dC ist ungerade und ist erfüllt. Beweis Klar: dC muss ungerade sein, sonst berühren sich maximale Kugeln. Die Bedingung ist notwendig und hinreichend für die Ausschöpfung der Wortmenge durch disjunkte Kugeln. Es gilt: Aus dem Satz konstruierte Tripel (n, M, dC) bedeuten noch nicht die Existenz eines zugehörigen Codes. Beispiele für 'perfekte Tripel' (n, M, dC) (n, qn, 1) — Alle Wörter sind Codewörter (n, 1, 2n + 1) — es gibt nur 1 Codewort (2n + 1, 2, 2n + 1) — es gibt 2 Codewörter Hamming-Codes Hq (r) (  , qn–r, 3)-Code     mit r  2 Golay-Codes G23 ist (23, 212, 7)-Code und G11 ist (11, 36, 5)-Code Andere perfekte Codes sind nicht bekannt (d.h. alle andern sind zu diesen äquivalent).   zurück zum Überblick Feel free to send me email: maria@oelinger.de
	© 2000 Maria Oelinger cand. math. Schranken Letzte Änderung: 12.12.2000 address: http://www.oelinger.de/maria/it_codi/schranken.htm