http://www.oelinger.de Home Maria Oelinger   sitemap
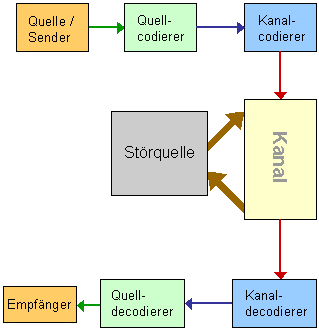
	zurück zur Übersicht Prüfungsprotokoll Hauptdiplomprüfung Mathematik Fach: Informationstheorie Prüfer: Prof. Dr. W. Luther, Universität Duisburg Datum: 29.11.2000 Dauer: ca. 35 Min Note: 1.0 Fachgespräch Was stellen Sie sich unter Quellencodierung und Kanalcodierung vor? Da fing ich an zu zeichen: Skizze 1 Quellcodierung bedeutet, Daten zu komprimieren. Kanalcodierung bedeutet, gute Decodierbarkeit zu gewährleisten, d.h. gute Fehlererkennungs- und Fehlerkorrekturmöglichkeiten. Quellcode ist z.B. der Huffman-Code, Kanalcodes sind die Blockcodes, z.B. Hamming- oder Golay-Code. Von der Quelle werden die Informationen (Nachrichten) abgeschickt, im Quellcodierer komprimiert und vom Kanalcodierer in den Kanal gesandt. 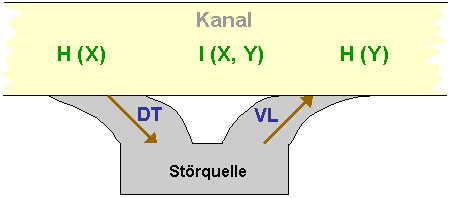Dort werden sie i.d.R. gestört, d.h. es kommt etwas von außen dazu (Rauschen), etwas anderes geht verloren. Im Kanaldecodierer werden die empfangenen Daten rekonstruiert, im Quellcodierer decodiert, so dass der Empfänger im Idealfall genau die gesendete Nachricht erhält. Skizze 2 Der Kanal wird gestört durch eine Störquelle (z.B. Rauschen beim Telefonieren). Über den Kanal gesendete Information ist die Transinformation I (X, Y), die Entropie H (X) ist auf der Senderseite zu finden, die Entropie H (Y) auf der Empfängerseite des Kanals.   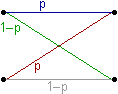Welche Arten von Kanälen gibt es? verlustloser Kanal VL Man teilt das Outputalphabet O = {y1, …, yt} auf in disjunkte Mengen B1, …, Bk, jede dieser Mengen enthält (oft 'falsche') Outputs, man kann alle diese Outputs eindeutig den ursprünglichen Inputs xi zuordnen deterministischer Kanal DT (Umkehrung zu VL) rauschfreier Kanal NL (noiseless channel) ist verlustlos und deterministisch (und nicht praxisnah) Abb f: S  O mit p (f (xi) | xi) = 1 VL, DT siehe auch Skizze 2 nutzloser Kanal identische Zeilen in der Kanalmtarix, gleiche Spaltenelemente:       Gibt es noch andere Arten von Kanälen? 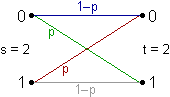Ja: Diskreter gedächtnisloser Kanal DGK mit Inputalphabet S, Outputalphabet O und Menge von Kanalwahrscheinlichkeiten p (yj | xi), wobei     j=1,…,t p (yj | xi) = 1 Kanalwahrscheinlichkeiten Kanalübertragungswahrscheinlichkeiten sind p (yj | xi): Die Wahrscheinlichkeit, dass yj empfangen wird beim Senden von xi. Zusammen beschrieben in der Kanalmatrix. Beispiel BSC binary symmetric channel   Woher kommen die gegebenen Wahrscheinlichkeiten? Gegeben ist neben der Kanalwahrscheinlichkeit auch die Eingangswahrscheinlichkeit p (xi). Sie werden statistisch ermittelt, z.B. zählt man die Häufigkeit von Buchstaben in Texten, nach 'q' kommt meistens 'u' usw.   Welche Wahrscheinlichkeiten interessieren uns noch? Die Wahrscheinlichkeit, dass x gesendet wurde, wenn y empfangen ist, nämlich die (rückwärts bedingte) Sendewahrscheinlichkeit p (x | y) = p (x, y) ÷ p (y)     (wenn p (y) > 0, sonst p (x | y) = p (x) ) mit der Verbundwahrscheinlichkeit p (x, y) = p (y | x) • p (x)   Wie kann ich wissen, was ich als gesendet annehmen soll? 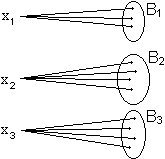Durch Entscheidungsschemata (partielle Abbildungen) f: O  C mit Mengen, für die f für das Output d richtig zum Codewort c hin decodiert: Bc := { d | f (d) = c } = { f –1 (c) } Ideal ist das Schema, wenn gilt: p (f (d) | d) = MaxcC p (c | d) Maximum-Likelihood-Entscheidungsschema ist f mit p (d | f (d)) = MaxcC p (d | c)     für alle Ausgabestrings d. Es gilt: Ist die Eingabe gleichverteilt, so ist das MLE-Schema ideal.   Was ist Gleichverteilung? Für ein Alphabet    S = {x1, …, xs}    gilt die Wahrscheinlichkeit p (xi) = 1/s   für alle i = 1, ..., s.   Wo tritt Gleichverteilung in der realen Welt auf? Oder anders: Wie sieht das bei Sprache aus?   Ist ganz und gar nicht gleichverteilt.   Wie sieht das bei Bildern aus?   Auch nicht. Kommt drauf an. Schon mehr gleichverteilt als Sprache ;-)   Welche Arten von Codes gibt es? variable und Blockcodes Linearcodes, zyklische Codes   Welche Eigenschaften können sie haben? 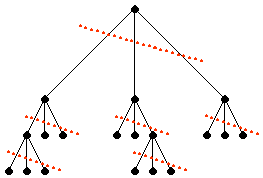optimal, perfekt, linear, zyklisch, (d – 1)-fehlererkennend, t-fehlerkorrigierend, komplett   Was ist ein kompletter Code? komplett heißt ein Präfixcode C, wenn für den zugehörigen Codebaum B = (K, P) gilt: B ist voll verzweigt, d.h. jeder Knoten hat keinen oder genau r Nachfolger. B ist reduzierbar auf die Wurzel durch sukzessives Abzwicken von vollen Gipfelknospen: i=1,…,n  = 1 gilt, d.h. Gleichheit bei Kraft-McMillan. Jedes Wort w  A* ist entweder Präfix eines Codeworts oder hat ein Codewort zum Präfix Die Anzahl der Codewörter hat die Form |C| = n = 1 + q • (r – 1) und die Längenverteilung L = {l1, …, ln} ist minimal, d.h. für L' = {l'1, …, l'n} gilt: l'i  li      =>      l'i = li   für alle i = 1, …, n Das Defizit e ist (beim quasikompletten Code) durch n + e = q • (r – 1) + 1 festgelegt.   Wie erzeugt man einen Linearcode? Mit der Generatormatrix G: L = { x • G | x  V (k, q) }, Fehler erkennt man mit der Kontrollmatrix; Standardformen; Fehlererkennung und -korrektur mittels Syndromdecodierung erklärt: (i-ter Einheitsvektor, abgezogen vom empfangenen Wort, ergibt wahrscheinlich gesendetes Codewort).   Wie kann man die Fehlereigenschaften verbessern?   z.B. durch Hinzufügen einer Paritätsstelle   Beispiele für Codes? Hamming Hq (r), Golay, Huffman   Wie ist der Minimalabstand bei Hamming-Codes?   d = 3 (leicht erkennbar bei Linearcodes wegen wC = d)   Ist das gut? Nicht schlecht, aber auch nicht sonderlich gut.   Wieso ist der Hamming-Code trotzdem so besonders?   Er ist perfekt.   Gibt es noch andere perfekte Codes? Ja, die beiden Golay-Codes G11 und G23, die haben sogar Mininmalabstände d = 5 und d = 7.   zurück zur Übersicht Feel free to send me email: maria@oelinger.de
	© 2000 Maria Oelinger cand. math. Prüfungsprotokoll Letzte Änderung: 04.12.2000 address: http://www.oelinger.de/maria/it_codi/protokoll_it.htm