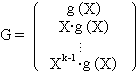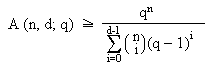http://www.oelinger.de Home Maria Oelinger   sitemap
	zurück zur Übersicht Prüfungsprotokoll Hauptdiplomprüfung Mathematik Fach: Codierungstheorie Prüfer: Prof. Dr. G. Törner, Universität Duisburg Datum: Nov 2000 Dauer: ca. 25 Min Note: 1.3   Fragenkatalog Was ist die Codierung allgemein, wozu dient sie, wozu nicht? Man möchte Daten übertragen, also an einem Ort möglichst einfach und originalgetreu rekonstruieren können, was an einem andern Ort ausgewählt und gesendet wurde. Sie dient nicht zur Verschlüsselung, denn das ist Kryptographie.   Inwiefern möchte man Codes optimieren? Sie sollen möglichst kurze Übertragungszeit bzw. Speicherplatz beanspruchen. Außerdem sollen sie einfach zu codieren sein und fehlertolerant.   Welche Codes kennen Sie überhaupt? Präfixcodes zum Beispiel, Huffman-Codes…   Welchen Präfixcode kennen Sie denn? Der Huffman-Code ist ein Präfixcode.   Kennen Sie noch mehr? Aus dem täglichen Leben? Telefonnummern!   Geben Sie ein allgemeines Modell an! Die Nachricht (x1, …, xk) wird codiert und zum Codewort (y1, …, yn), wobei n > k, da z.B. Prüfziffern hinzukommen. Dieses Wort schicke ich durch einen Kanal (z.B. Telefonleitung). Auf der andern Seite erhalte ich den Vektor (y1', …, yn'), der evtl. etwas anders aussieht als das gesendete Wort, da der Kanal gestört sein kann (und meist auch ist). Dieses empfangene Wort schicke ich durch meinen Decodierer und erhalte schließlich (x1', …, xk'). Im Idealfall ist dies die ursprüngliche Nachricht.   Das führt zu einem speziellen Code, welcher ist das? Ein Blockcode, genauer: (n, k)-Blockcode. Das ist ein Quadrupel (X, Y, E, D) mit nichtleeren Mengen X und Y (die heißen Alphabete) und Abbildungen E: Xk  Yn   (injektiv) sowie D: Yn  Xk   (surjektiv). Wieviele Elemente haben die Alphabete?  In der Praxis endlich viele. Wieviele Elemente haben sie denn meistens?  Zwei (Binärcodes).   Welche Aussagen kann man machen, wenn man die Werte des (n, k)-Blcokcodes kennt? Man kann die Informationsrate k/n bzw. 1/n • log q M angeben, die ein Maß dafür ist, wieviel Information durch den Code vermittelt werden kann. Je näher sie bei 1 liegt, desto mehr Information kommt rüber.   Was spricht gegen eine hohe Informationsrate? Die Fehleranfälligkeit, d.h. der Unterschied zwischen den einzelnen Codewörtern ist dann sehr gering, so dass durch gestörte Übertragung aufgetretene Fehler nicht erkannt werden können. Das kann man durch den Minimalabstand beschreiben: Es gibt (n, M, d; q)-Codes mit Wortlänge n, Codewortanzahl M, Minimalabstand d und q-närem Alphabet als Grundlage. Zunächst definiert man den Hamming-Abstand d(x, y) := | {i | xi  yi} | dann sucht man den Hamming-Abstand d, der minimal ist für alle Abstände zwischen allen Codewörtern.   Jetzt kommt die Frage nach optimalen und perfekten Codes. Dazu eine weitere Definition: A (n, d; q) = Max {M | Es ex. ein (n, M, d; q)-Code} Ist M = A (n, d;  q), so heißt der Code optimal. Für den perfekten Code betrachtet man die Kugelpackungsschranke: d = 2e + 1 bedeutet, ich kann e Fehler korrigieren. Sei ein (n, M, 2e + 1; q)-Code gegeben. Dann gilt: Erreicht ein Code diese Schranke (d.h. Gleichheit), so heißt er perfekt. Welche perfekten Codes kennen Sie?  Golay G23 und G11 und den Hamming-Code. Kennen Sie noch mehr?  Nein, man kennt nur diese. Können Sie die Schranke näher erläutern? Klar, ich definiere Kugeln um jedes Codewort, die disjunkt sind: Sei Ke(z) = {u  Xn | d (u, z)  e} für alle z  C. Dann sind für x  y die Kugeln Ke(x) und Ke(y) disjunkt (sonst gäbe es v  Ke(x)  Ke(y) mit d (x, y)  d (x, v) + d (v, y)  2e WID zu d (x, y)  d = 2e + 1)  • (q – 1)i    ist Anzahl der Vektoren u  Xn mit d (z, u) = i. Also enthält jede Kugel genau    i=0,…,e  • (q – 1)i    Elemente. Daraus folgt die Behauptung.   Welche Arten von Codes gibt es noch? Ein Linearcode bildet einen Unterraum des Vektorraums GF (q)n. Es sind [n, k, d; q]-Codes mit Wortlänge n, Dimension bzw. Anzahl der Informationsstellen (wie im Modell ganz oben) k, dem Minimalabstand d und einem q-nären Alphabet. Es gilt: M = qk. Außerdem ist bei Linearcodes das Minimalgewicht gleich dem Minimalabstand. Das Gewicht eines Codeworts ist die Anzahl der Koordinaten ungleich Null. Das Minimalgewicht eines Codes ist das Minimum dieser Werte (natürlich ohne Nullvektor). Die Struktur des Unterraums erlaubt eine gute Handhabung, leider gibt es aber nur wenige optimale Linearcodes. Wie beschreibt man einen solchen Code hinreichend? Man gibt die Generatormatrix an, die man wie folgt darstellen kann: G = ( Ek | A ), entsprechend dazu die Kontrollmatrix H = ( –At | En – k ). Die Zeilen von G bilden eine Basis des zugehörigen Codes C. Wie sieht dann der Code aus?    C = { x  GF (q)n | H • xt = 0 }   Gibt es überhaupt lineare Codes, die optimale sind? Ja, den Hamming-Code. Er wird auf verschiedene Arten definiert, z. B. über den Minimalabstand. Sei k  N, q Primpotenz. Dann kann ich den Vektorraum GF (q)k in n := qk – 1 / q – 1 disjunkte Klassen zerlegen, indem ich in jeder Klasse gerade die Vielfachen eines Vektors aus GF (q)k \ {0} zusammenfasse. Dann nehme ich aus jeder Klasse einen Vertreter und konstruiere mir damit die Matrix H = (h1 … hn), für die gilt: Je zwei Spalten sind linear unabhängig und damit ist die minimale Anzahl für linear abhängige Spalten 3. Diese Matrix kann man als Kontrollmatrix eines [n, n – k, 3; q]-Codes verstehen, das ist der (n, n – k)-Hamming-Code.   Es gibt noch eine andere Klasse von Codes. Welche? Die zyklischen Codes. Dabei erzeugt ein Wort, z.B. 10110, den Code, indem ich es shifte, d.h. dass 01011 und alle andern Shifts wieder Codewörter sind. Die Generatormatrix dazu ist wobei man Codewörter auch als Polynome verstehen kann: 10110 entspricht dann dem Polynom 1 + x2 + x3 und der Shift wird realisiert durch Multiplikation mit x. Also: xi • g (x) Wie sieht denn der Shift für das Codewort aus? Das ist eine Permutation  (ai) = an für i = 1 und  (ai) = ai – 1 für i = 2, …, n. Beschreiben Sie den Code explizit! C = <S> mit S = {v,  (v), …, n – 1 (v)}, C ist also lineare Hülle der Menge S. Für n (v) bekommt man wieder v, da v das erzeugende Element dieser endlichen Menge ist, d.h. primitives Element. Das ganze spielt sich ja im Körper GF (q) ab mit q = pr Primpotenz. Für r = 1 ist GF (p) gerade Zp.   Sagen Sie etwas über Prüfzeichencodes. Nur allgemein und ein Beispiel. Man benutzt Permutationen, die, angewandt auf die Koordinaten meines Wortes, eine Kontrollgleichung erfüllen sollen. z.B. ISBN-Code mit der Kontrollgleichung a10 i=1,…,9 i • ai mod 11 Machen Sie die Gleichung homogen. Da stand ich auf dem Schlauch. Erwartet wurde: 0  i=1,…,9 i • ai mod 11 – a10 War aber nicht so wichtig. Was ist denn der zugrundeliegende Körper? GF (q). Und hier? GF (11), aber mit der Ausnahme, dass nur a10 = 10 vorkommen darf, die andern Koordinaten können maximal 9 sein. Wie sieht die Kontrollmatrix aus? Sie enthält die Zeilen ri  xi mod 11 und für den homogenen Fall (d.h. wenn man das als Gleichungssystem lösen will): Zeilen ri wie oben mit zusätzlicher letzter Spalte, die gerade die Summe i=1,…,9 i • ai mod 11 – a10 enthält.   Nochmal zu den Schranken: Kennen Sie noch andere als die Kugelpackungsschranke? Klar, die Singleton-Schranke: A (n, d; q)  qn – d + 1 Gilt Gleichheit, heißt der Code MDS-Code. Die Plotkin-Schranke: Für  = (q – 1) / q und d > n gilt: A (n, d; q)  d / (d – n) Für q = 2: A (n, d; q)  2d / (2d – n) Und die untere Schranken (bisher waren es ja ausschließlich obere Schranken) von Gilbert-Varshamov: die der Kugelpackungsschranke ähnlich ist, außer dass sie in der Summe bis d – 1 geht, das ist die Anzahl der Fehler, die ich erkennen kann.   Schließlich noch etwas zu Code-Modifikationen Erweitern Neue letzte Komponente (negative Paritätssumme) für Codewörter einfügen, z.B. bei Prüfzeichencodierung. Punktieren Gegenteil von Erweitern: Letzte Komponente streichen Vergrößern Weitere Wörter dem Code hinzufügen, z.B. Einsvektor zur Generatormatrix hinzufügen, denn dann hab ich eine bessere Struktur, da mit jedem Wort das Komplement enthalten ist. Verkleinern geeignet Codewörter entfernen, z.B. nur solche mit geradem Gewicht behalten. Verlängern Vermehren der Informationsstellen (Dimension und Länge erhöhen) Verkürzen Informationsstelle streichen an gleichen Stellen in Codewörtern, die dort übereinstimmen, z.B. bei verkürzten RS-Codes, wo man die s letzten Stellen streicht, wenn es Nullen sind und nur diese Wörter in den neuen Code aufnimmt.   zurück zur Übersicht Feel free to send me email: maria@oelinger.de
	© 2000 Maria Oelinger cand. math. Prüfungsprotokoll Letzte Änderung: 04.12.2000 address: http://www.oelinger.de/maria/it_codi/protokoll_it.htm